[CTF Writeup] Fun with Finite Fields
At the TROOPERS Conference 2019 there was a Capture the Flag Challenge, where I worked on the “Fun with Finite Fields” problem.
The only prior information about the challenge is the name: “Fun with Finite Fields” - OK probably Elliptic Curve cryptography…
How the challenge works: Link to heading
We find the lonely challenge server waiting for my TCP connection. I get this prompt after connecting with netcat:
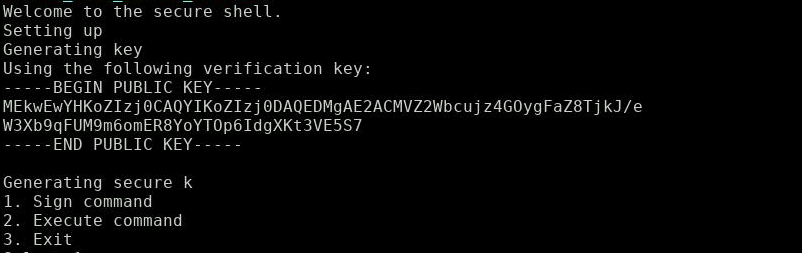
Note the display of the public key - we will need that for later.
‘Generating secure k’ - What a surprise, this is probably the textbook example I was thinking about. How the attack works will unfold shortly, but let’s look first what the server has to offer.
Two commands of interest:
- Sign command: Enter a command and retrieve it’s EC crypto signature.
- Execute command: Enter a command and it’s signature and retrieve it’s output.

You can only retrieve the signatures for the commands [’ls’, ‘pwd’, ‘cat server.py’].
Alright, let’s execute ‘ls’:

ls shows: the flag is right there we just need to cat it
Pretty straight forward: The challenge clearly wants us to forge a signature for a ‘cat flag.txt’ command.
Let’s see what server.py looks like (execute ‘cat server.py’):
import ecdsa
import os
import sys
import secrets
print("Welcome to the secure shell.")
print("Setting up")
print("Generating key")
sk = ecdsa.SigningKey.generate() # uses NIST192p
vk = sk.get_verifying_key()
print("Using the following verification key:")
print(vk.to_pem().decode('utf-8'))
"""https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm#Security says it is important to have a secure random k
so make sure we generate it properly"""
print("Generating secure k")
k = secrets.randbelow(sk.curve.order)
def sign():
allowed_cmds = ['ls', 'pwd', 'cat server.py']
cmd = input("Command to sign:")
if cmd not in allowed_cmds:
print("Illegal command, only allowed commands are %s" % allowed_cmds)
else:
sig = sk.sign(cmd.encode("utf-8"), k=k)
print("Signature: %s" % sig.hex())
def execute():
cmd = input("Command to execute: ")
signature = input("Signature: ")
signature = bytes.fromhex(signature)
try:
vk.verify(signature, cmd.encode('utf-8'))
print("Correct signature, executing command")
os.system(cmd)
except ecdsa.BadSignatureError:
print("Invalid signature")
return
menu = {
'1': sign,
'2': execute,
'3': sys.exit
}
while True:
print("1. Sign command")
print("2. Execute command")
print("3. Exit")
cmd = input("Select:")
try:
menu[cmd]()
except KeyError:
print("Invalid selection")
The textbook vulnerability is right there: k is not generated randomly for each signature but only once and reused for different signatures!
BTW: Nice hint in the code:
https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm
It states there:
As the standard notes, it is not only required for k to be secret, but it is also crucial to select different k for different signatures, otherwise the equation in step 6 can be solved for the private key.
The solution: Link to heading
All we need to do is follow the instructions on Wikipedia:

Let’s resolve the symbols here:
- n : group order (all operations are mod n)
- k : cryptographically secure random integer from [1,n-1]
- z : SHA1(message) mod n, where message will be signed (SHA1 is default)
- (r, s) : the signature of message (yes the signature is a tuple)
How the attack works: Link to heading
Using the public key from the greeting message, we can infer n, the group order.
We just need to parse the public key, which is best done within python-ecdsa.
We also need to parse the 2 signatures we obtained from the ‘ls’ and ‘cat server.py’ commands.
Additionally we compute z and z’ by hashing ‘ls’ and ‘cat server.py’ with SHA1.
We can then compute k and finally the private key.
Using the private key, we finally can forge signatures to commands of our choice.
Attack and results: Link to heading
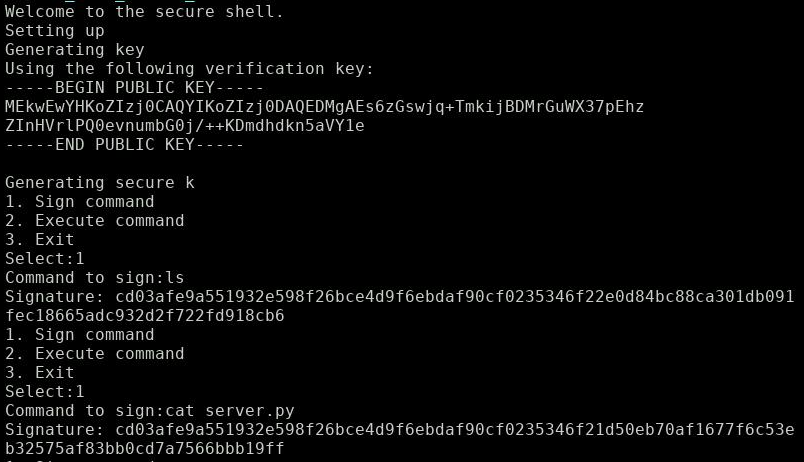
Let’s feed the public key and the 2 signatures into our python script:
import ecdsa
import gmpy
pub_key_string = "MEkwEwYHKoZIzj0CAQYIKoZIzj0DAQEDMgAEs6zGswjq+TmkijBDMrGuWX37pEhzZInHVrlPQ0evnumbG0j/++KDmdhdkn5aVY1e"
m1 = "ls"
sig1 = "cd03afe9a551932e598f26bce4d9f6ebdaf90cf0235346f22e0d84bc88ca301db091fec18665adc932d2f722fd918cb6"
m2 = "cat server.py"
sig2 = "cd03afe9a551932e598f26bce4d9f6ebdaf90cf0235346f21d50eb70af1677f6c53eb32575af83bb0cd7a7566bbb19ff"
# Generate own key-pair to access utility functions
sk = ecdsa.SigningKey.generate() # uses NIST192p
vk = sk.get_verifying_key()
# Parse public key from the server and obtain n
veri_key = vk.from_pem(pub_key_string)
n = veri_key.pubkey.order
# Parse the 2 signatures
r1, s1 = ecdsa.util.sigdecode_string(bytes.fromhex(sig1), order=n)
r2, s2 = ecdsa.util.sigdecode_string(bytes.fromhex(sig2), order=n)
# Hash the commands (ls, cat server.py) and transform them into numbers
h1 = ecdsa.keys.sha1(m1.encode("utf-8"))
z1 = ecdsa.util.string_to_number(h1.digest())
h2 = ecdsa.keys.sha1(m2.encode("utf-8"))
z2 = ecdsa.util.string_to_number(h2.digest())
# Perform math according to wikipedia
k=((z1 - z2) * gmpy.invert(s1 - s2, n)) % n
print("k: ", k)
r_inv = gmpy.invert(r1,n)
d_a = ((s1*k - z1) * r_inv) % n
# Sign own command (cat flag.txt) using the obtained secret exponent
COMMAND = "cat flag.txt"
sk_new = sk.from_secret_exponent(d_a)
print("Command: ", COMMAND)
sig = sk_new.sign(COMMAND.encode("utf-8"), k=k)
print("Signature: ", sig.hex())
The forged signature to our own command (‘cat flag.txt’) is presented to the server:

There we are: We hold the flag in our hands
That’s it: The flag is right there!
All in all I must say, the only big challenge was to fiddle with python-ecdsa to parse the public key and signatures.
It’s nice to work with python-ecdsa and get familiar with the library since I have not worked much with Elliptic Curve cryptography.
I definitely learned alot about the framework and how use it.
I hope someone will find help in the textbook implementation of this attack.